Implementing Mixture of Experts Layers
Part 6 of Jaxformer (Part 5: Distributed Training | Part 7: Training Results)
Mixture of Experts (MoE) layers scale LLMs by routing tokens to a small subset of feedforward experts, reducing memory use while enabling larger models. Here we show an implementation as well as address the main training challenges such as stability, expert collapse, and accelerator efficiency.
Motivation and Challenges
A recent advancement in scaling LLMs to larger networks has been through the introduction of Mixture of Experts (MoE) modules in the decoder. Training MoE models are primarily difficult for 2 reasons. The first, is due to training stability. This involves ensuring each expert gets roughly the same number of tokens otherwise, it can lead to expert collapse. Luckily for us, the hard work is done and lots of open-source models provide strong training recipes that we can use. The second is training efficiency, as you want to ensure that you are utilizing your accelerators to their max, and they aren’t idle while training. We will be writing MoE similar to the DeepseekV3 paper. Additionally, distributed techniques such as expert parallelism are not being included, but we provide a general overview on how to incorporate it. Below are images representing this architecture.
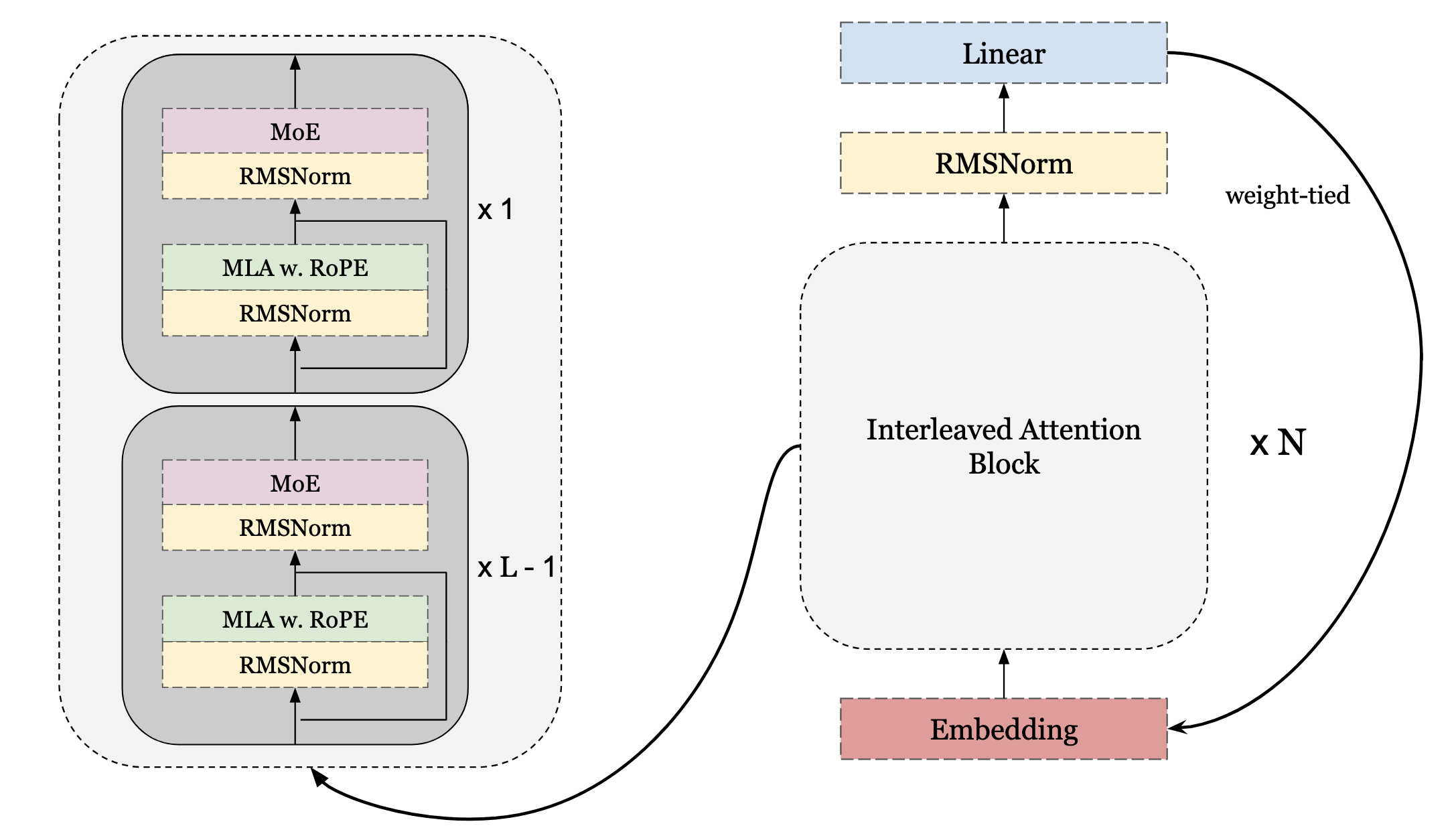
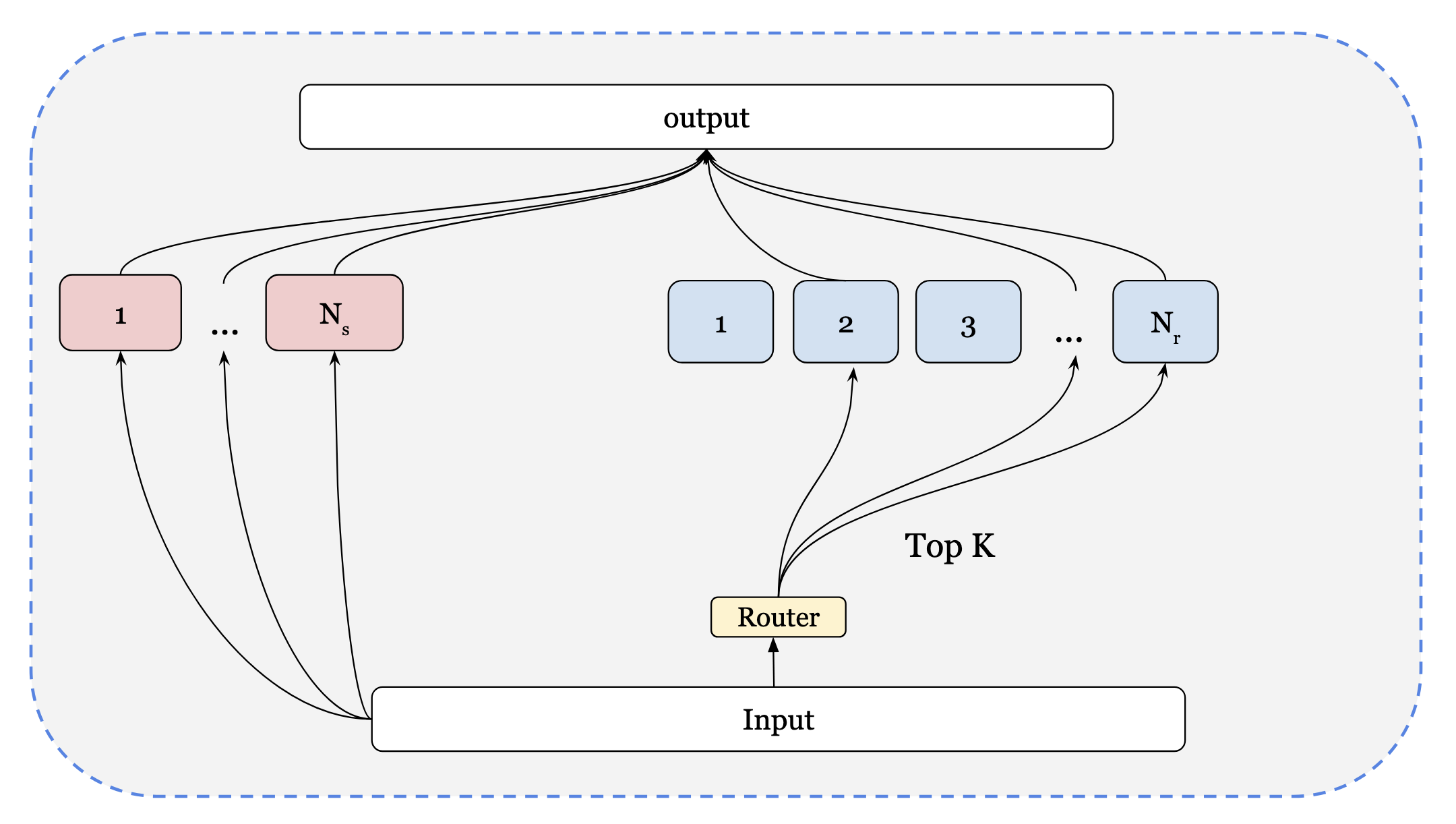
Router Design
We first begin by writing the router and layer module whilst integrating it into the current program by writing the distributed setup and training configs.
Scoring and All-Gather
The router decides how to send each token by computing a score. In the DeepSeek-V3 paper, they describe the score of the $i$ expert for the $t$ token as
\[s_{i,t} = \sigma \left(u_t^Te_i\right)\]where $\sigma$ is the Sigmoid activation function. This can essentially be written as a dense layer with no bias since our tokens are transposed by definition due to being row-wise vectors. For simplicity, we also include the bias in our score function even though it has been shown at larger scales $>100B$ params that they tend to cause training instabilities. The vectors for each expert $e$ are known as the centroids, so theDense network can be described as one as well.
The term centroids comes from the idea that we take the dot product with the center of mass of each expert and then select the top-$k$ tokens by similarity.
We begin the router by defining the parameters and centroids network.
class NoisyKGate(nn.Module):
n_experts: int
k: int
model_dtype: jnp.dtype
def setup(self):
self.centroids = Dense(features=self.n_experts, dtype=self.model_dtype)
The __call__ method, accumulates the scores and all-gathers them for two reasons. The first is that when we apply a top-k selection to chose the top experts, we need all the results along the channel-dim. The second reason and also why we do not perform a traditional all-to-all, is that when determining the routing, we want to compute it across all time steps. It is therefore easier to have the scores replicated along the tensor axis.
class NoisyKGate(nn.Module):
...
def __call__(self, x: Array) -> Tuple[Array, Array, Array]:
local_scores = nn.sigmoid(self.centroids(x))
scores = jax.lax.all_gather(
local_scores,
"tp",
axis=x.ndim - 1,
tiled=True,
) # ( B, T, C) fully collected
Top-k Selection
Now, we can write the function to select the top_k experts. We select the top k of the given array x, receiving indices and scores of those values, defining them as g values. For the indices chosen, we normalize the scores and return back normalized scores alongside the indices.
class NoisyKGate(nn.Module):
...
def top(self, x: Array) -> Tuple[Array, Array]:
g_i, i = jax.lax.top_k(x, self.k)
g = g_i / jnp.sum(g_i, axis=-1)
return g, i
We can then apply this function using jax.lax.apply_along_axis to vmap over the first 2 axes and obtain the g_scores, indices arrays for the batch (size will be (B, T, self.k) for both).
class NoisyKGate(nn.Module):
...
def __call__(self, x: Array) -> Tuple[Array, Array, Array]:
g_scores, indices = jnp.apply_along_axis(func1d=self.top, axis=-1, arr=scores)
return g_scores, indices, scores
MoE Implementation
Now, we proceed to the main MoE implementation. A standard implementation of MoE isn’t too difficult; however in JAX, there are caveats such as trying to avoid using for loops making an MoE implementation more difficult. We provide a simpler implementation based on Google large-scale implementation , combined with the idea from DeepSeek-V3.
Shared Experts and Routing
We start by defining our class with standard parameters.
class MoE(nn.Module):
model_dimension: int
n_shared: int
n_experts: int
k: int
dropout_rate: float
capacity_factor: float = 1.0
model_dtype: jnp.dtype = jnp.float32
@nn.compact
def __call__(self, x, train=True):
...
We first pass x through the shared experts described in the DeepSeek-V3 script, which are essentially n feed-forward dimensions. Thus, we can create a Dense layer of size n_shared × model_dimension, then split and sum it across the n_shared dimension.
class MoE(nn.Module):
...
@nn.compact
def __call__(self, x, train=True):
B, T, C = x.shape
shared = Dense(
features=self.model_dimension * self.n_shared,
dtype=self.model_dtype,
)
res_shared = shared(x)
res_shared = rearrange(res_shared, "B T (n d) -> B T n d", n=self.n_shared)
res_shared = jnp.sum(res_shared, axis=2) # (B, T, n, d) -> (B, T, d)
...
Then, we setup the router and get the scores and auxiliary values from the router’s forward pass.
class MoE(nn.Module):
...
@nn.compact
def __call__(self,x,train=True):
...
router = NoisyKGate(
n_experts=self.n_experts,
k=self.k,
model_dtype=self.model_dtype,
)
g_scores, indices, scores = router(x) # (B, T, k), (B, T, k), (B, T, n_experts)
Note that x is still split across the tensor dim, but the scores are not. We now compute the capacity per expert. Ideally when training, we want the tokens to be evenly spilt between all experts however that is quite rare and hence we allow some extra space through the capacity factor of the tokens.
def __call__(self, x, train=True):
...
capacity = B * T
if train:
capacity = int(capacity * self.capacity_factor / self.n_experts)
Scatter and Expert Inputs
Now, we need to build the expert inputs which will be in the shape of(n_experts, capacity, C) describing the input to each expert. For this we write the scatter function. This is inspired by the routing logic in the Google MoE layers linked above and provides a pure-JAX way to determine and create the expert routing. We begin by reshaping the inputs into 2D Tensor: one for channels and the rest is treated like a batch dim.
class MoE(nn.Module):
def scatter(
self, x: Array, scores: Array, indices: Array, capacity: int
) -> Tuple[Array, Array]:
B, T, C = x.shape
x = x.reshape(B * T, C)
scores = scores.reshape(B * T, self.k)
indices = indices.reshape(B * T, self.k)
Since we are trying to essentially determine for each expert the first N tokens where N is the capacity, we first sort the tokens by the highest score of the batch. There are other techniques to determine the priority but this is the simplest one for now. Note we don’t sort for each position since we want every batch to remain in row with its top-k.
def scatter(...):
...
# sort to arrange in order of expert scores for each batch by
# the highest scored expert
sorted_token_idx = jnp.argsort(-scores[:, 0], axis=0)
sorted_indices = jnp.take_along_axis(indices, sorted_token_idx[:, None], axis=0)
sorted_scores = jnp.take_along_axis(scores, sorted_token_idx[:, None], axis=0)
Now we swap the axes and flatten to essentially get our order in terms of priority across all batches, that is all tokens for the first position, then second position all the way until the $k$ position.
def scatter(...):
...
# swapping gives you the highest highest score across the batch
# expert_1: [b_1, b_2, .. b_{B * T }], expert_2: [b_1, b_2, .. b_{B * T }], ...
# flatten then to get expert indices in order
flat_indices = jnp.swapaxes(sorted_indices, 0, 1).reshape(-1)
flat_scores = jnp.swapaxes(sorted_scores, 0, 1).reshape(-1)
We now convert to one hot encodings to let us know for each position which expert it is from and multiply with the scores to get a score map
def scatter(...):
...
# convert to one hot encoding
# then multiply to get the score for each instead of 1
expert_onehot = jax.nn.one_hot(flat_indices, self.n_experts, dtype=jnp.int32) # (B*T*k, n_experts)
expert_scores = flat_scores[:, None] * expert_onehot # (B*T*k, n_experts)
Now, we perform a cumulative sum. Instead of having a 1 for expert i, it now says which token number it is en-queue for that expert. We can also take the max across the experts to get how many tokens are going to each expert. This is a useful statistic to determine if we avoided expert-collapse.
def scatter(...):
...
position_in_expert = jnp.cumsum(expert_onehot, axis=0) * expert_onehot # get which position it is in the expert
# find max position across all batches since that is the total sum from cumsum
tokens_per_expert = jnp.max(position_in_expert, axis=0) / (B * T) # take average across batch
Now that we have the position in expert, we perform the inverse operations to get back our original (B x T, k) input with a new axis that represents the position in the expert.
def scatter(..):
...
# reshape it back to get for
# expert_i: [b_1, b_2, .. b_{B * T }] where b_i is the one hot for which position it is in
# same for expert scores
position_in_expert = position_in_expert.reshape(self.k, B * T, self.n_experts)
expert_scores = expert_scores.reshape(self.k, B * T, self.n_experts)
# go back to orginal shape
position_in_expert = jnp.swapaxes(position_in_expert, 0, 1) # (B*T, k, n_experts)
expert_scores = jnp.swapaxes(expert_scores, 0, 1) # (B*T, k, n_experts)
Since for each k only one field in n_experts is non-zero (as it was originally a one-hot encoding), we can take the max across k to determine, for every batch, which expert it is routed to and at what position. We subtract 1 to zero-index it. This is done by taking jnp.max(position_in_expert, axis=1), where axis=1 corresponds to the top-k routed experts. We can then apply argsort on sorted_token_idx, which performs an inverse permutation and restores the original arrangement of our batches.
def scatter(...):
...
# for every batch in each expert find the non-zero expert position
# as for every expert we only have one non-zero value
final_pos = jnp.max(position_in_expert, axis=1) - 1 # make it 0 indexed
final_scores = jnp.max(expert_scores, axis=1) # do the same for the score
# unsort the indices
unsorted_indices = jnp.argsort(sorted_token_idx)
final_pos = jnp.take_along_axis(final_pos, unsorted_indices[:, None], axis=0)
final_scores = jnp.take_along_axis(
final_scores, unsorted_indices[:, None], axis=0
)
We can now create a dispatch mask which will one hot encode the position of the capacity each token is in. Subtracting 1 from the max is helpful here because the tokens are zero-indexed. This ensures that tokens which were originally 0, before subtracting 1, (eg. not routed to any expert) will not be one-hot encoded. Same goes for the tokens that are greater than or equal to the capacity (row will be all 0).
def scatter(...):
...
# final pos is now the orginal order where each index is the position in the expert
# if it is greater than or less than the capcity / 0 (hence -1) the row will be 0 in the capcity
# hence we have for each positoin and expert the one hot tells us which position it is in
# if it is in
dispatch_mask = jax.nn.one_hot(
final_pos, capacity, dtype=jnp.int32
) # (B*T, n_experts, capacity)
# multiply out all the values in the capcity by final score
# we can replicate since at most 1 value will be non zero
scores_mask = (
dispatch_mask * final_scores[..., None]
) # (B*T, n_experts, capacity)
For every expert at position c in the capacity, we can sum the input vector for every batch since at most, only 1 value across the batch is at that position. For this we use einsum, summing over the b dim.
def scatter(...):
# since only one expert at every position in capactiy at most
# we can sum to get rid of batch dim and get the exepect capacity dimension indicies
expert_inputs = jnp.einsum("bd,bec->ecd", x, dispatch_mask)
return expert_inputs, scores_mask, tokens_per_expert
Expert Execution and Aggregation
The expert inputs now have shape (experts, capacity, dimension), allowing us to proceed with the main call. Note that the scores correspond to g_scores, since these are what we want in the score mask (the coefficients for the weighted sum of the experts). We then create a single expert using a FeedForward module. Then we apply a linen lifted transformation, nn.vmap, which is equivalent to vmap but operates directly over a module (in this case, the expert). While we have generally avoided using lifted transformations from Flax, in this case it is simpler to rely on Flax rather than writing a separate module with parameters and manually applying jax.vmap over them.
@nn.compact
def __call__(self, x, train=True):
...
expert_inputs, score_mask, tokens_per_expert = self.scatter(
x, g_scores, indices, capacity
) # (e, c, d) , (B * T, e, c), (e,)
expert = FeedForward(
model_dimension=self.model_dimension,
dropout_rate=self.dropout_rate,
model_dtype=self.model_dtype,
)
expert_outputs = nn.vmap(
lambda expert, inp: expert(inp, train=train),
in_axes=(0),
out_axes=(0),
variable_axes={"params": 0},
split_rngs={"params": True, "dropout": True},
)(expert, expert_inputs) # (n_experts, capacity, d)
We sum the outputs with the score mask across all experts and capacity, since only one position in the capacity of each expert can be non-zero. Our goal is to aggregate the outputs for every batch position, weighted by the corresponding score. That is, at time step $i$, the final expert output $x_i$ is
\[x_i = \sum_{j}^{N} g_{i,j}e_{j}\]where $e_j$ is output for the $j$ expert when the input was routed to expert $j$.
@nn.compact
def __call__(self, x, train=True):
...
expert_outputs = jnp.einsum("ecd,tec->td", expert_outputs, score_mask)
expert_outputs = expert_outputs.reshape(B, T, C)
Auxiliary Loss
In order to prevent expert collapse, DeepSeek-V3 adds an auxiliary loss to the main CE loss in order to penalize routing tokens to the same expert. The auxiliary loss is defined as
\[L_e = \alpha \sum_{i=1}^{N} f_i P_i\]where $\alpha$ is a hyperparameter and $N$ is the number of experts. Then, $f_i, P_i$ are defined as follows
\[f_i = \frac{N}{kT} \sum_{t=1}^T \mathbb{1} (s_{i,t} \in \text{TopK}(\{ s_{j,t} \mid 1 \leq j \leq N \}, K))\]where $s_{i,t}$ is the unnormalized score, essentially counting how many times for that expert the score is in the top $k$ and $P_i$ is the sum of the normalized scores,
\[P_i = \frac{1}{T} \sum_{t=1}^T S_{i,t}\]where $S_{i,t} = \frac{s_{i,t}}{\sum_{j=1}^{N} s_{j,t}}$. Thus we can compute $f, P$ as a function and return it as a metric. This promotes a uniform distribution over experts since it penalizes each expert for being used more times ($f_i$ becomes larger).
We first begin by computing $P$. We normalize the scores to get $S$, and then reshape into 2D arrays since we can treat B as a time dim. Then we need to sum over this batch/time dim (axis=0) and normalize by T = B x T_batch. Thus, $P$ will then be of shape (n_experts, ).
class MoE(nn.Module):
...
def auxiliary_loss(self, scores: Array, indices: Array) -> Array:
B, T, n_experts = scores.shape
scores = scores / jnp.sum(scores, axis=-1, keepdims=True)
scores = scores.reshape(B * T, n_experts)
p = jnp.sum(scores, axis=0) / (B * T)
...
We now calculate f by first flattening it into a one-dimensional array, since we want to count across the entire batch and time steps, the number of indices that were routed to each head. We do this by applying jax.nn.one_hot, giving a tensor of shape (B × T × k, n_experts). Then, we sum over the first dim and normalize across the batch. We apply the other factor of $\frac{N}{k}$ when computing the loss in the main.py script. Note the tokens_per_expert we previously computed is the same statistic, but for clarity we will explicitly compute it for now.
class MoE(nn.Module):
def auxiliary_loss(self, ...):
...
total_batch = B * T * self.k
indices = indices.reshape(total_batch)
f = jax.nn.one_hot(indices, n_experts, dtype=jnp.float32)
f = jnp.sum(f, axis=0) / (B * T)
return f,p
Once we have the auxiliary loss, we can now structure our final output as the output and statistics for the MoE layer.
@nn.compact
def __call__(self, x, train=True):
f, p = self.auxiliary_loss(scores, indices)
aux = {"tokens_per_expert": tokens_per_expert, "f": f, "p": p}
x = res_shared + expert_outputs
return expert_outputs, aux
Integration into the Transformer
Now, we modify our layer block, encoder block and sharded model to incorporate the moe aux. For ease in training, we only make it so that the last layer in the interleaved RoPE blocks use the MoE outputs. In this layer, we add the necessary params as well as a flag for use_moe defaulted to False.
class Layer(nn.Module):
model_dimension: int
n_heads: int
T: int
latent_dim: int
dhR: int
n_experts: int
k: int
n_shared: int
capacity_factor: float
use_moe: bool = False
dropout_rate: float = 0.1
model_dtype: jnp.dtype = jnp.bfloat16
In the call, we use the flag to determine which block type is needed and return the auxiliary value along with the cache. Then, in the call, we can use the flag to determine which block type is needed and return the auxiliary value along with the cache.
class Layer(nn.Module):
...
@nn.compact
def __call__(
self, x, cache: Optional[cache_type] = None, train=True
) -> Tuple[Array, cache_type]:
...
x_res = x
if self.use_moe:
x, aux = MoE(
model_dimension=self.model_dimension,
n_experts=self.n_experts,
k=self.k,
n_shared=self.n_shared,
capacity_factor=self.capacity_factor,
dropout_rate=self.dropout_rate,
model_dtype=self.model_dtype,
)(x, train=train)
else:
x, aux = FeedForward(
model_dimension=self.model_dimension,
dropout_rate=self.dropout_rate,
model_dtype=self.model_dtype,
)(x, train=train), None
x = x + x_res
return x, (cache, aux)
In the block, we can take the MoE parameters and pass them into every layer, where the last sets the parameteruse_moe=True.
class Block(nn.Module):
layers: int
model_dimension: int
n_heads: int
T: int
latent_dim: int
dhR: int
n_experts: int
k: int
n_shared: int
capacity_factor: float
dropout_rate: float = 0.1
model_dtype: jnp.dtype = jnp.bfloat16
@nn.compact
def __call__(
self, x, cache: Optional[cache_type] = None, train=True
) -> Tuple[Array, cache_type]:
...
moe_stat = None
for i in range(self.layers):
# build cache
...
x, (cache_out, aux) = Layer(
model_dimension=self.model_dimension,
n_heads=self.n_heads,
T=self.T,
latent_dim=self.latent_dim,
dhR=self.dhR if i < self.layers - 1 else 0,
n_experts=self.n_experts,
k=self.k,
n_shared=self.n_shared,
capacity_factor=self.capacity_factor,
use_moe=(i == self.layers - 1), # moe on last layer
dropout_rate=self.dropout_rate,
model_dtype=self.model_dtype,
)(x, current_cache, train=train)
if aux is not None:
moe_stat = aux
...
...
return x, (out_cache, moe_stat)
We now have to store and return moe_stat inside the pipeline stage of the shardedModel. Note we do not implement MoE into the base transformer although it is simpler then the implementation we show in the shardedModel.
We can also keep an array inside the pipeline function to store the moe_stats.
def pipeline(...):
...
moe_stat = []
for i in range(microbatches + layers - 1):
...
state, (out_cache, out_moe_stat) = jax.vmap(fn)(
state_idx, state, stage_params, current_cache, layer_keys
)
...
moe_stat.append(out_moe_stat)
Now we can stack all the layers to obtain a shape of (M + L - 1, layers_per_device, n_experts) for each metric. Since every MoE layer returns n_experts, and jax.vmap stacks them across layers_per_device, this results in M + L - 1 calls yielding this shape.
def pipeline(...):
...
moe_stat = jax.tree.map(
lambda *x: jnp.stack(x, axis=0),
*moe_stat
)
Unlike the cache, we cannot simply return this because the cache is used as a placeholder. In cases where the computation is not in the main pipeline, the results don’t matter which implies that we never have to consider slicing it. However, for moe_stat, we don’t actually want the full M + L - 1 statistics since this will be used in the loss and we only care about the M microbatches that are passed in. Moreover, these are not simply the first M calls, they are offset for each layer. For the first layer, we use the first M arrays, for the second layer, we use the M arrays from indices 1 to M + 1, and so on similar to pipeline parallelism where each layer is offset according to its position. To do this, we can make a function called slice_moe which is applied with a map over the moe_stat dict. Then, for each array, we can use a function each_layer which maps over the layer_per_device axis (axis=1) and applies a dynamic slice based on the layer index. For each layer we can use the layer_idx to apply jax.lax.dynamic_slice_in_dim which as mentioned in the RoPE module, is essentially equivalent to arr[..., start_idx: start_idx + length] on some axis. Our start index is the sum of all the past layers and the layer index of the current layer. The length is microbatches long since each layer processes M microbatches continuously. We can then mean over the microbatches since they are equivalent to time dimensions like before (only we have spilt it up instead of having one large batch).
def pipeline(...):
...
def slice_moe(x: Array) -> Array:
def each_layer(layer_idx, x):
return jax.lax.dynamic_slice_in_dim(
x,
layers_per_device * device_idx + layer_idx,
microbatches,
axis=0
)
sliced_x = jax.vmap(each_layer, in_axes=(0, -2), out_axes=(-2))(jnp.arange(layers_per_device), x)
return sliced_x
moe_stat = jax.tree.map(
lambda x: slice_moe(x).mean(axis=0), # mean across microbatches
moe_stat
)
...
We can then multiply out the f and p stats since we only need them for the loss. Additionally we can sum the tokens per expert across the different layers.
def pipeline(...):
moe_stat = {
"tokens_per_expert": moe_stat["tokens_per_expert"].sum(axis=0), # (experts,)
"aux_loss": moe_stat['f'] * moe_stat['p'], # (layers_per_device, experts)
}
return outputs, (out_cache, moe_stat)
The last place in model.py where we need to change from MoE is in the partition spec. We also need to shard the kernel in the MoE expert layer since the linen.vmap will add an extra dim which our rules don’t account for. We only have to update the layer_partition since that contains the MoE layer.
def pipeline(...):
...
join_fn = lambda path: " ".join(i.key for i in path).lower()
def layer_partition(key: Tuple[str, ...], x: Array) -> P:
path = join_fn(key)
if "moe" in path and "feedforward" in path:
if x.ndim == 4:
return P("pp", None, "tp", "dp")
if x.ndim == 3:
return P("pp", None, None)
if "gamma" in path or "beta" in path:
return P("pp", None, None, "tp")
if x.ndim == 3:
return P("pp", "tp", "dp")
return P("pp", None)
...
layer_p_spec = jax.tree.map_with_path(
layer_partition,
eval_shape[1],
)
return embed_p_spec, layer_p_spec
We can also add a helper function to count the total and active parameters. We count the total parameters similar to the main script function. Then we use the join_fn to check whether the layer is an expert layer, and if so, we count only k experts instead of all n_experts.
def param_count(self, params):
total_params = jax.tree.reduce(
lambda x, y: x + y.size,
params,
0,
)
join_fn = lambda path: " ".join(i.key for i in path).lower()
def count_active_params(key, x):
path = join_fn(key)
n_elements = x.size
is_expert = "moe" in path and "feedforward" in path
if is_expert:
n_elements = n_elements // self.cfg.n_experts * self.cfg.k
return n_elements
active_params_map = jax.tree.map_with_path(count_active_params, params[1])
active_params = jax.tree.reduce(
lambda x, y: x + y, active_params_map, 0
)
return total_params, active_params
Training Integration
We can then also update the modelConfig in utils.py.
@dataclass
class modelConfig:
"""model config class"""
model_dimension: int
vocab_size: int
n_head: int
blocks: int
layers_per_block: int
T: int
latent_dim: int
dhR: int
dropout_rate: float = 0.1
model_dtype: str = "bfloat16"
k: int = 0
n_experts: int = 0
n_shared: int = 0
capacity_factor: float = 1.0
Now we make the changes to our main training script. The first change is using the correct parameter count.
def main(cfg):
...
param_count, active_param_count = model.param_count(params)
log(f"Total parameters: {param_count:,} with {active_param_count:,} active")
...
Inside of our loss_fn in step we unpack with an extra state.
def step(params, x, y, key, train):
def loss_fn(params, x, y, key):
logits, (_, moe_stat) = model.pipe_step(
params,
x,
key=key,
train=train,
)
We can then sum across the different device axes and add it to our loss.
def step(...):
def loss_fn(...):
...
loss_balance = 0.0
moe_stat = jax.tree.map(lambda x: jax.lax.psum(x, axis_name="dp"), moe_stat)
moe_stat = jax.tree.map(lambda x: jax.lax.psum(x, axis_name="tp"), moe_stat)
moe_stat = jax.tree.map(lambda x: jax.lax.psum(x, axis_name="pp"), moe_stat)
loss_balance = (cfg.model_config.n_experts / cfg.model_config.k) * moe_stat["aux_loss"].sum()
loss = loss_cross + cfg.alpha * loss_balance
metrics = {
"loss": loss,
"loss_cross": loss_cross,
"loss_balance": loss_balance,
"load_expert": moe_stat["tokens_per_expert"]
}
return loss, metrics
The wandb logging can be updated.
for current_step in range(init_step, total_steps):
...
if use_wandb:
wandb_log = {
"step": current_step,
"loss/train_loss": metrics["loss"],
"loss/train_cross_entropy_loss": metrics["loss_cross"],
"lr": opt_state[1].hyperparams["learning_rate"],
}
wandb_log["loss/load_loss"] = metrics["loss_balance"]
for h in range(cfg.model_config.n_experts):
wandb_log[f"load/head_{h}"] = jax.device_get(metrics[f"load_expert"])[h]
if current_step % cfg.checkpoint_steps == 0:
...
if use_wandb:
wandb_log["loss/val_loss"] = val_metrics["loss"]
wandb_log["loss/val_cross_entropy_loss"] = val_metrics["loss_cross"]
wandb_log["loss/val_load_loss"] = val_metrics["loss_balance"]
for h in range(cfg.model_config.n_experts):
wandb_log[f"load/head_{h}"] = jax.device_get(val_metrics[f"load_expert"])[h]
...
Now, we move to launch the final training run across 32 TPU-v4s.