How to Write the Base Model

Part 2 of Jaxformer (Part 1: Tokenization | Part 3: Sharded Model)

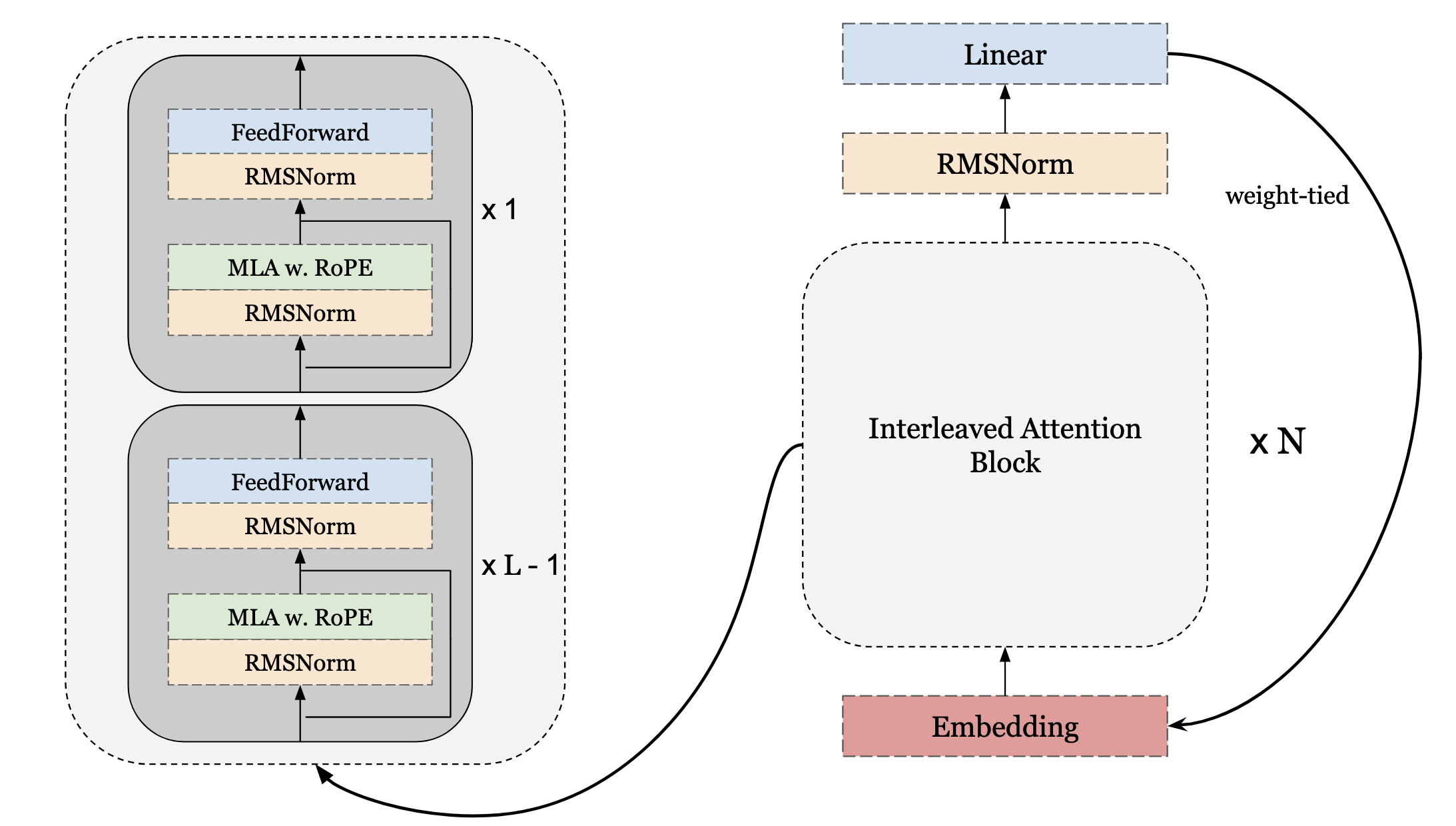
We begin by writing the single-TPU base model including modern day modules such as RMSNorm, Multi-latent Attention, RoPE, decoupled RoPE embeddings, interleaved attention, KV-cache and more. This serves as a working foundation, from which we can later scale to multi-TPU and distributed training setups.

Here is the base architecture we will building and reflects many of the components in modern-day transformers.

Root-Mean Squared Norm

In our model, we utilize root-mean squared norm (RMS Norm) as the normalization between layers. In JAX we can initialize models directly within the forward pass, similar to TensorFlow. Since this is lazy initialization, we only need to specify the input dtype at the start.

import flax.linen.nn as nn

class RMSNorm(nn.Module):
    model_dtype: jnp.dtype = jnp.float32

Our init/forward pass is defined under the nn.compact decorator. We begin by computing the mean of the squared values and scale by its square root. Next, we initialize the shift/scale parameters and apply them to obtain the output (note: Some RMSNorm implementations do not use shift parameters). These parameters are broadcasted across the (B, T) dimensions, while the last axis of the input x is treated as the channel dim.

class RMSNorm(nn.Module):
    model_dtype: jnp.dtype = jnp.float32

    @nn.compact
    def __call__(self, x: Array) -> Array:
        rms = jnp.mean(jnp.square(x), axis=-1, keepdims=True)
        x = x / jnp.sqrt(rms + 1e-6)

        gamma = self.param(
          "gamma",
          nn.initializers.ones,
          (1, 1, x.shape[-1]),
          self.model_dtype
        )

        beta = self.param(
          "beta",
          nn.initializers.zeros,
          (1, 1, x.shape[-1]),
          self.model_dtype
        )

        x = x * gamma + beta

        return x

Embedding

Embedding Lookup

The embedding layer helps convert tokens into continuous $n$ dimensional vectors. For this class, we can use JAX’s flexibility when initializing our class using a PyTorch init pattern in the setup method.

class Embeddings(nn.Module):
    model_dimension: int
    vocab_size: int
    model_dtype: jnp.dtype

    def setup(self):
        self.embedding = nn.Embed(
            num_embeddings=self.vocab_size,
            features=self.model_dimension,
            dtype=self.model_dtype,
        )
        self.norm = RMSNorm(model_dtype=self.model_dtype)

nn.Embed is a built-in class capable of performing an embedding lookup as well as weight-typing which can be used to convert vectors to a distribution over tokens. Additionally, the norm can be used in this final layer. Thus, we separate our call function into two control-flows, one for the start of the forward pass and one for the end based on a param out.

def __call__(self, x: Array, out: bool = False) -> Array:
    if not out:
        # perform embedding loop
    else:
        # perform dot-product with transpose of the embedding params
    return x

For the embedding lookup we can pass our input x = self.embedding(x) through the layer.

def __call__(self, x: Array, out: bool = False) -> Array:
    if not out:
        x = self.embedding(x)
        # perform embedding loop
    else:
        # perform dot-product with transpose of the embedding params

    return x

A caveat of JAX is that the first forward-pass must initialize all the params, so we can pass our input through the norm as a dummy pass to initialize it.

def __call__(self, x: Array, out: bool = False) -> Array:
    if not out:
        x = self.embedding(x)
        # perform embedding loop
        if self.is_mutable_collection("params"):
            _ = self.norm(x)
    else:
        # perform dot-product with transpose of the embedding params

    return x

Weight Tying

For the second-pass (weight-tying) we first pass x through the norm and then use the built in embed.attend(x) function to perform the transposed matmul. Our final embedding class is shown below.

class Embeddings(nn.Module):
    model_dimension: int
    vocab_size: int
    model_dtype: jnp.dtype

    def setup(self):
        self.embedding = nn.Embed(
            num_embeddings=self.vocab_size,
            features=self.model_dimension,
            dtype=self.model_dtype,
        )
        self.norm = RMSNorm(model_dtype=self.model_dtype)

    def __call__(self, x: Array, out: bool = False) -> Array:
        if not out:
            x = self.embedding(x)
            if self.is_mutable_collection("params"):
                _ = self.norm(x)
        else:
            x = self.norm(x)
            x = self.embedding.attend(x)
        return x

FeedForward

We can use the standard nn.Dense module to implement a Feedforward block. We wrap the nn.Dense for now since this will allow us to perform Tensor Parallelism / FSDP in the future as it is the building block for all future modules.

class Dense(nn.Module):
    features: int
    dtype: jnp.dtype = jnp.float32

    @nn.compact
    def __call__(self, x: Array):
        x = nn.Dense(features=self.features, dtype=self.dtype)(x)
        return x

For the FeedForward layer we combine 2 Dense modules using a 4x up/down projection.

class FeedForward(nn.Module):
    model_dimension: int
    ff_dim: int
    dropout: float
    model_dtype: jnp.dtype

    @nn.compact
    def __call__(self, x: Array, train: bool = True) -> Array:
        x = Dense(
            features=self.ff_dim,
            dtype=self.model_dtype,
        )(x)
        x = nn.gelu(x)
        x = Dense(
            features=self.model_dimension,
            dtype=self.model_dtype,
        )(x)
        x = nn.Dropout(rate=self.dropout)(x, deterministic=not train)
        return x

Note that since JAX is functional, for features such as Dropout, we pass parameters to allow the functions to remain pure, rather then relying on state.

RoPE

Mathematical Intuition

Rotary Positional Embeddings allow for relative embeddings based on applying standard euclidean 2D-rotation to each $2$ dimensional subspaces of the $n$ dimensional vector. We can represent this as

\[\mathbf{x}_{\text{RoPE}}(m) = \underbrace{ \begin{bmatrix} \cos(m\theta_1) & -\sin(m\theta_1) & 0 & 0& \ldots & 0 & 0\\ \sin(m\theta_1) & \cos(m\theta_1) & 0 & 0 & \ldots & 0 & 0 & \\ 0 & 0 & \cos(m\theta_2) & -\sin(m\theta_2) & & \vdots & \vdots \\ 0 & 0 & \sin(m\theta_2) & \cos(m\theta_2) & & \vdots & \vdots \\ \vdots & \vdots & & & \ddots & \vdots & \vdots \\ 0 & 0& \ldots & \ldots & & \cos(m\theta_{d/2}) & -\sin(m\theta*{d/2}) \\ 0 & 0 & \ldots & \ldots & & \sin(m\theta*{d/2}) & \cos(m\theta*{d/2}) \end{bmatrix} }* \begin{bmatrix} x_1 \\ x_2 \\ \vdots \\ x_d \end{bmatrix}\]

where $m$ is the time position. We can also define $R(m \theta_k)$ block as

\[R(m\theta_k) = \begin{bmatrix} \cos(m\theta_k) & -\sin(m\theta_k)\\[2pt] \sin(m\theta_k) & \cos(m\theta_k) \end{bmatrix}.\]

and then in paired coordinates $(2k-1,2k)$:

\[\begin{bmatrix} x'_{2k-1}\\ x'_{2k} \end{bmatrix} = R(m\theta_k) \begin{bmatrix} x_{2k-1}\\ x_{2k} \end{bmatrix}, \qquad k=1,\dots,\tfrac{d}{2}.\]

Intuitively, this is just a 2D-rotation by different angles at each time step, applied within each subspace to provide every possible time step with a distinct relative positional encoding.

The rotation matrix is used in the forward pass; however, instead of doing a matrix multiplication which would be $O(d^2T)$, we can perform a product-wise multiplication taking advantage of the of the sparsity of the matrix and achieve $O(dT)$. Hence for any time step and position, we only perform 2 multiplications which can be written as an element-wise operation instead.

\[\begin{equation} \mathbf{x}'(m) = \begin{pmatrix} x*1 \\ x_2 \\ x_3 \\ x_4 \\ \vdots \\ x*{d-1} \\ x*d \end{pmatrix} \odot \begin{pmatrix} \cos m\theta*{1} \\ \cos m\theta*{1} \\ \cos m\theta*{2} \\ \cos m\theta*{2} \\ \vdots \\ \cos m\theta*{d/2} \\ \cos m\theta\_{d/2} \end{pmatrix} - \begin{pmatrix} * x_2 \\ x_1 \\ * x_4 \\ x_3 \\ \vdots \\ * x*d \\ x*{d-1} \end{pmatrix} \odot \begin{pmatrix} \sin m\theta*{1} \\ \sin m\theta*{1} \\ \sin m\theta*{2} \\ \sin m\theta*{2} \\ \vdots \\ \sin m\theta*{d/2} \\ \sin m\theta*{d/2} \end{pmatrix} \end{equation}\]

Implementation in JAX

To implement this, we can create the cosine and sine vectors and then perform the necessary tensor ops on $x$ during the forward pass. We begin the class like a standard JAX module; however, unlike the others, this will have no params in it. We just use this class to allow for lazy initialization with the other classes that call it, such as Multi-Head Latent Attention.

We first begin by taking in T (the length of the sequence) and the model_dim, ensuring that the dimension can be split into 2 subspaces.

class RoPE(nn.Module):
    T: int
    model_dim: int

    def setup(self):
        assert self.model_dim % 2 == 0, "model_dim must be even"

Then, we create a frequency array [1,2,3,...,T] which will scale our $\theta$. To make this a2D array, we expand the dim to create [[1], [2], [3], ..., [T]], since this will allow for broadcasting with the channel frequencies and make it one indexed.

freq = jnp.arange(self.T, dtype=jnp.float32)[:, None] + 1

To setup the $\theta$, we first create an array of the powers of the base that yield each $\theta$. Specifically, $\theta_i = B^{-2i/d}$ , so we can represent the array as

\[[\theta_1, \theta_2, \ldots, \theta_{d / 2}] = B^{-2/d \cdot [1,2,\ldots, d/2]}.\]

Since our final array for $\sin/\cos$ is $\sin \left([\theta_1, \theta_1, \theta_2, \theta_2, \ldots, \theta_{d / 2}, \theta_{d/2}]\right)$ , we can repeat the elements along the second dim and then flatten it into one continuous array. Thus,

\[pos = [0,0,1,1, \ldots, d/2, d/2].\]

pos = jnp.arange(self.model_dim // 2, dtype=jnp.float32)[:, None]
pos = pos.repeat(2, axis=-1).reshape(1, -1)

We now compute our base (we use $10,000$) to create our array of $\theta$ , using log rules.

log_theta_base = jnp.log(10000.0)
theta = jnp.exp(-2 * pos / self.model_dim * log_theta_base)

Finally, we create the final array of $\cos$ and $\sin$ by broadcasting each channel dim across every time step $t$ where each $\theta$ now becomes $t\theta$. The final array will therefore be

\[[[1 \theta_0, 1\theta_0 1\theta_1, \theta_1, \ldots, 1 \theta_{d/2} 1 \theta_{d/2}], \ldots, [T \theta_0, T \theta_0, \ldots, T \theta_{d/2}, T \theta_{d/2}]].\]

class RoPE(nn.Module):
    T: int
    model_dim: int
    def setup(self):
        assert self.model_dim % 2 == 0, "model_dim must be even"

        freq = jnp.arange(self.T, dtype=jnp.float32)[:, None] + 1

        pos = jnp.arange(self.model_dim // 2, dtype=jnp.float32)[:, None]
        pos = pos.repeat(2, axis=-1).reshape(1, -1)
        log_theta_base = jnp.log(10000.0)
        theta = jnp.exp(-2 * pos / self.model_dim * log_theta_base)

        self.cos = jnp.cos(freq * theta)
        self.sin = jnp.sin(freq * theta)

In the forward pass, $x$ is batched across $t$ time steps, allowing us to index into the 2D array and perform element-wise multiplication. Therefore, we first begin by taking in our array as well as the time step our array begins at to determine the first index. We also get the $T$ or length of our input to know how far to index into the $\sin / \cos$ arrays. We also cast the input to float32 to help with precision.

def __call__(
    self,
    x: Array,
    t_start: int,
) -> Array:
    B, T, C = x.shape
    x_dtype = x.dtype
    x = x.astype(jnp.float32)

Since the $\cos$ Hadamard product requires the input x, we can perform that operation before turning our attention to the second operand.

cos_rope = x * self.cos[t_start : t_start + T, :]

We first begin by breaking the $x$ input into the 2 dim subspaces and multiplying the second component by $-1$. We then stack the second onto the first and reshape to obtain the flipped version.

x_inter = x.reshape((B, T, C // 2, 2))
x_inter_one = x_inter[..., 0] # first component
x_inter_two = -1 * x_inter[..., 1] # second component
x_inter = jnp.stack([x_inter_two, x_inter_one], axis=-1) # stack will switch betwen on the given axis, in this case this is a flip
x_inter = x_inter.reshape((B, T, C))

We can then multiply this by the $\sin$ array, add it back and recast to the original type to get our output.

class RoPE(nn.Module):
    T: int
    model_dim: int

    def setup(self):
        assert self.model_dim % 2 == 0, "model_dim must be even"

        freq = jnp.arange(self.T, dtype=jnp.float32)[:, None] + 1

        pos = jnp.arange(self.model_dim // 2, dtype=jnp.float32)[:, None]
        pos = pos.repeat(2, axis=-1).reshape(1, -1)
        log_theta_base = jnp.log(10000.0)
        theta = jnp.exp(-2 * pos / self.model_dim * log_theta_base)

        self.cos = jnp.cos(freq * theta)
        self.sin = jnp.sin(freq * theta)

    def __call__(
        self,
        x: Array,
        t_start: int,
    ) -> Array:
        B, T, C = x.shape
        x_dtype = x.dtype
        x = x.astype(jnp.float32)

        cos_rope = x * self.cos[t_start : t_start + T, :]

        x_inter = x.reshape((B, T, C // 2, 2))
        x_inter_one = x_inter[..., 0]
        x_inter_two = -1 * x_inter[..., 1]
        x_inter = jnp.stack([x_inter_two, x_inter_one], axis=-1)
        x_inter = x_inter.reshape((B, T, C))

        sin_rope = x_inter * self.sin[t_start : t_start + T, :]

        x = cos_rope + sin_rope
        x = x.astype(x_dtype)

        return x

Multi-Latent Attention

Low-Rank Attention Motivation

We now write the core attention mechanism of the model. We will use multi-latent attention introduced in DeepSeek-V2. The driving idea is motivated by how to save inference-time memory. In a standard KV-cache, our transformer has to save $2LTd$ elements as for each key/value pair in a layer, we have $T$ time steps for which the dimension is $d$. Now, consider a transformer with a sequence length of $T = 128k$, dimension of $d = 7168$ and layers $L = 61$. If the KV cache is stored in bfloat16 this leads to $\frac{2 \cdot 61 \cdot 128 \cdot 10^3 \cdot 7168 \cdot 2}{10^9} \approx 220GB$ of memory constraints. There exists solutions to optimize this such as Grouped Query Attention or Multi Query Attention (when $n_{\text{groups}}$ equals 1); however, these often lead to a decrease in quality. Multi latent attention attempts to fix this using the idea of Low-Rank decomposition . Instead of using $K = W^k x$ and $V = W^v x$. we decompose the $W^k$ and $W^v$ into a matrix-matrix product $W^K = AB$ where $A \in \mathbb{R}^{d \times r}$ and $B \in \mathbb{R}^{r \times d}$ where $r « d$. This way we use $2dr$ space instead of $2d^2$ and thus grow linearly with $d$ instead of quadratically. In terms of the cache, we now store $Bx$ instead of $W^Kx = ABx$. This means our memory is now $2LTr$, which in terms of the previous example, is roughly $33$ GB.

To further save memory, we can use the same $B$ matrix for the key and values, thus $W^K = A^KB$ and $W^V = A^V B$. This means we can get rid of the 2 factor, further cutting our memory in half to $\approx 16$GB. Note this does trade memory for compute; however, in these cases, we are memory bound which appeals to the idea of MLA.

Implementation and Caching

Thus we begin by defining our module, with our hyper-parameters.

class MLA(nn.Module):
    model_dimension: int
    n_heads: int
    T: int
    latent_dim: int
    dhR: int
    model_dtype: jnp.dtype
    dropout: float = 0.0

model_dimension, n_head, dropout, model_dtype all follow from standard MHA. Latent dim is the rank $r$ of the low-rank projection. dhR and T are for the RoPE embedding which will be discussed later.

For our call method, we take in the array as well as the caches.

@nn.compact
def __call__(
  self,
  x: Array,
  *,
  cKV_cache: Optional[Array] = None,
  kRT_cache: Optional[Array] = None,
  train=True,
) -> Tuple[Array, Tuple[Optional[Array], Optional[Array]]]:

  B, T, C = x.shape # get dimension information

Note we will return a tuple with the result of the attention and another tuple which will hold the caches for the key-value pair and the RoPE (to be discussed later on).

We first begin by projecting the x to the latent dim for the key-value pair and the queries.

x = Dense(features=2 * self.latent_dim, dtype=self.model_dtype)(x)
kv_latent, q_latent = jnp.split(x, 2, axis=-1)

Note that we only create one Dense for this operation since we can split the output along the last dim due to obtaining $x \in \mathbb{R}^{ B \times T \times 2 \cdot r}$ which is equivalent to doing the following:

kv_latent = Dense(features=self.latent_dim, dtype=self.model_dtype)(x)
q_latent = Dense(features=self.model_dimension, dtype=self.model_dtype)(x)

We can then write the up-projection from the latent space to the final key, value, query pairs.

k, v = jnp.split(
  Dense(features=2 * self.model_dimension, dtype=self.model_dtype)(kv_latent),
  2,
  axis=-1,
)
q = Dense(features=self.model_dimension, dtype=self.model_dtype)(q_latent)

Then, we can map over the tuple (q, k ,v) to split them into n_head batches.

q, k, v = jax.tree.map(
  lambda x: rearrange(x, "B T (nh d) -> B nh T d", nh=self.n_heads), (q, k, v)
)

We make use of the rearrange op from the einops library for ease of reading the operation, as opposed to writing x.reshape(...).permute(...). In this case, we split the last dim into n_head arrays and then permute it to ensure the last 2 dims will be multiplied like in MHA. We can use the tree.map function to map over the the tuple.

We can now write a function to perform the normal scaled-dot product attention.

def scaledDotProd(q, k, v, mask):
  input_dtype = q.dtype

  q, k ,v = jax.tree.map(lambda x: x.astype(jnp.float32), (q, k, v))
  dk = q.shape[-1]

  w = jnp.einsum("B n T d, B n t d -> B n T t", q, k) * (dk**-0.5)
  w = jnp.where(mask == 0, -jnp.inf, w)
  w = jax.nn.softmax(w, axis=-1)
  output = jnp.einsum("B n T t, B n t d -> B n T d", w, v)

  output = output.astype(input_dtype)
  return output

Breaking this function down, the input dtype is recorded to ensure that after performing the attention computation in jnp.float32, it can be casted back to the right precision afterwards. We then covert our q,k,v to jnp.float32. The attention operation can be expressed using einsum notation and casted back to the original type.

We can then create the mask and call the function.

mask = jnp.tril(
  jnp.ones((B, self.n_heads, q.shape[2], k.shape[2])),
)

output = scaledDotProd(q, k, v, mask)

After, we can use rearrange to concat all the heads back together, pass it through a projection matrix and apply Dropout.

output = rearrange(output, "B nh T dk -> B T (nh dk)")
output = Dense(features=self.model_dimension, dtype=self.model_dtype)(output)
output = nn.Dropout(rate=self.dropout)(output, deterministic=not train)

MLA also uses the idea of decoupled RoPE appending on the positional encoding to the absolute key-query pairs. We first project $x$ into a latent RoPE space and encode those using the previous RoPE module. We can then concat them to the keys / queries. Since we will be using interleaved blocks (some layers will not have positional embeddings), we use a check for rope if the rope latent dim dhR is greater than 0.

use_rope = self.dhR > 0

if use_rope:
  t_start = 0 # needed for KV Cache
  x_k_r = Dense(features=self.dhR, dtype=self.model_dtype)(x)
  x_q_r = Dense(features=self.dhR * self.n_heads, dtype=self.model_dtype)(x)

Following the Deepseek V-3 paper, each query head will get a unique set of decoupled RoPE encodings but the key heads will all share one set (repeated across each head). Now, we can setup a RoPE module and apply them onto both latents. For the queries RoPE, we can rearrange them to split each head into it’s own batch.

if use_rope:
  t_start = 0 # needed for KV Cache
  x_k_r = Dense(features=self.dhR, dtype=self.model_dtype)(x)
  x_q_r = Dense(features=self.dhR * self.n_heads, dtype=self.model_dtype)(x)

  rope_k = RoPE(
    model_dim=self.dhR, T=self.T
  )
  rope_q = RoPE(
    model_dim=self.dhR * self.n_heads,
    T=self.T,
  )

  kRt = rope_k(x_k_r, t_start)

  qRt = rope_q(x_q_r, t_start)
  qRt = rearrange(qRt, "B T (nh d) -> B nh T d", nh=self.n_heads)

After constructing the key, query, and value tensors, if we are using RoPE, we can concatenate them while repeating the decoupled key embeddings across all heads.

q, k, v = jax.tree.map(
  lambda x: rearrange(x, "B T (nh d) -> B nh T d", nh=self.n_heads),
  (q, k, v)
)

if use_rope:
  q = jnp.concatenate([q, qRt], axis=-1)

  kRt = jnp.repeat(kRt[:, None, :, :], self.n_heads, axis=1) # add dim for head
  k = jnp.concatenate([k, kRt], axis=-1)

The last step is to setup the caching. The first change is in the RoPE block to find t_start since if we are using cached indices, we need to know which position to begin applying the RoPE from. To do this, we take the length of the cache as it represents our current index which we need to start from as tensor-indexing is 0-indexed.

Thus our first line in the if statement of the rope block becomes:

t_start = KV_cache.shape[1] if KV_cache is not None else 0

Note we can use either KV_cache.shape[1] or KR_cache.shape[1].

Then we can build the cache if we are not training.

if not train:
# build cache

If the past cache isn’t none, we want to append along the $T$ axis which is the 1 index, otherwise we want to set it to the kv_latent. Thus, a simple implementation allows us to set the kv_latent to the concat of the KV_cache if it is not none and the current latent as it will be of length 1 (since we are using the past key/value from the cache). We can then set the KV_cache to this.

x = Dense(features=2 * self.latent_dim, dtype=self.model_dtype)(x)
kv_latent, q_latent = jnp.split(x, 2, axis=-1)
...
if not train:
  if KV_cache is not None:
    kv_latent = jnp.concatenate([KV_cache, kv_latent], axis=1)
  KV_cache = kv_latent

The same approach can work with the RoPE keys.

if not train:
  if KV_cache is not None:
    kv_latent = jnp.concatenate([KV_cache, kv_latent], axis=1)
  KV_cache = kv_latent

  if use_rope:
    if KR_cache is not None:
      kRt = jnp.concatenate([KR_cache, kRt], axis=1)
    KR_cache = kRt

The last change required is in the masking since if we have a length of 1, we don’t want to mask out any element since that query pair can attend to every past one.

if T == 1:
  # q.shape[2] is 1 as well but we are more explict
  mask = jnp.ones((B, local_n_heads, 1, k.shape[2])) l
else:
  mask = jnp.tril(
    jnp.ones((B, local_n_heads, q.shape[2], k.shape[2])),
  )

At the ending, we return following the signature of the function:

return output, (KV_cache, KR_cache)

To improve the readability of the signatures in the future, we can use a type alias of:

cache_type = Tuple[Optional[Array], Optional[Array]]

Thus the final MLA class is:

class MLA(nn.Module):
    model_dimension: int
    n_heads: int
    T: int
    latent_dim: int
    dhR: int
    model_dtype: jnp.dtype
    dropout: float = 0.0

    @nn.compact
    def __call__(
        self,
        x: Array,
        *,
        KV_cache: Optional[Array] = None,
        KR_cache: Optional[Array] = None,
        train=True,
    ) -> Tuple[Array, cache_type]:
        use_rope = self.dhR > 0

        B, T, C = x.shape

        x = Dense(features=2 * self.latent_dim, dtype=self.model_dtype)(x)
        kv_latent, q_latent = jnp.split(x, 2, axis=-1)

        if use_rope:
            t_start = KV_cache.shape[1] if KV_cache is not None else 0
            x_k_r = Dense(features=self.dhR, dtype=self.model_dtype)(x)
            x_q_r = Dense(features=self.dhR * self.n_heads, dtype=self.model_dtype)(x)

            rope_k = RoPE(
                model_dim=self.dhR, T=self.T
            )
            rope_q = RoPE(
                model_dim=self.dhR * self.n_heads,
                T=self.T,
            )

            kRt = rope_k(x_k_r, t_start)

            qRt = rope_q(x_q_r, t_start)
            qRt = rearrange(qRt, "B T (nh d) -> B nh T d", nh=self.n_heads)

        if not train:
            if KV_cache is not None:
                kv_latent = jnp.concatenate([KV_cache, kv_latent], axis=1)
            KV_cache = kv_latent

            if use_rope:
                if KR_cache is not None:
                    kRt = jnp.concatenate([KR_cache, kRt], axis=1)
                KR_cache = kRt

        k, v = jnp.split(
            Dense(features=2 * self.model_dimension, dtype=self.model_dtype)(kv_latent),
            2,
            axis=-1,
        )
        q = Dense(features=self.model_dimension, dtype=self.model_dtype)(q_latent)

        q, k, v = jax.tree.map(
            lambda x: rearrange(x, "B T (nh d) -> B nh T d", nh=self.n_heads), (q, k, v)
        )

        q, k, v = jax.tree.map(
            lambda x: jax.lax.all_to_all(
                x, "tp", split_axis=1, concat_axis=3, tiled=True
            ),
            (q, k, v),
        )

        if use_rope:
            qRt = jax.lax.all_to_all(qRt, "tp", split_axis=1, concat_axis=3, tiled=True)
            q = jnp.concatenate([q, qRt], axis=-1)

            kRt = jnp.repeat(kRt[:, None, :, :], self.n_heads, axis=1)
            kRt = jax.lax.all_to_all(kRt, "tp", split_axis=1, concat_axis=3, tiled=True)
            k = jnp.concatenate([k, kRt], axis=-1)

        def scaledDotProd(q, k, v, mask):
            input_dtype = q.dtype

            q, k ,v = jax.tree.map(lambda x: x.astype(jnp.float32), (q, k, v))
            dk = q.shape[-1]

            w = jnp.einsum("B n T d, B n t d -> B n T t", q, k) * (dk**-0.5)
            w = jnp.where(mask == 0, -jnp.inf, w)
            w = jax.nn.softmax(w, axis=-1)
            output = jnp.einsum("B n T t, B n t d -> B n T d", w, v)

            output = output.astype(input_dtype)
            return output

        local_n_heads = q.shape[1]
        if T == 1:
            mask = jnp.ones((B, local_n_heads, 1, k.shape[2]))
        else:
            mask = jnp.tril(
                jnp.ones((B, local_n_heads, q.shape[2], k.shape[2])),
            )

        output = scaledDotProd(q, k, v, mask)

        output = jax.lax.all_to_all(
            output, "tp", split_axis=3, concat_axis=1, tiled=True
        )
        output = rearrange(output, "B nh T dk -> B T (nh dk)")

        output = Dense(features=self.model_dimension, dtype=self.model_dtype)(output)
        output = nn.Dropout(rate=self.dropout)(output, deterministic=not train)

        return output, (KV_cache, KR_cache)

Interleaved Attention Layers

The idea of interleaved attention layers was introduced in Cohere’s Command A model. There they use sliding window attention with positional embeddings (RoPE) and a full attention with no positional embeddings. Here we use MLA attention for all layers in the block with decoupled RoPE but don’t apply RoPE at the ending. This is relatively simple as we take a layer-per-block and on the last one, set the dhR = 0. The class is shown below.

We begin with the single layer which applies the pre-norm normalization, attention and feedforward network.

class Layer(nn.Module):
    model_dimension: int
    n_heads: int
    T: int
    latent_dim: int
    dhR: int
    dropout_rate: float = 0.1
    model_dtype: jnp.dtype = jnp.bfloat16

    @nn.compact
    def __call__(
        self, x, cache: Optional[cache_type] = None, train=True
    ) -> Tuple[Array, cache_type]:
        x_res = x

        x = RMSNorm(model_dtype=self.model_dtype)(x)
        x, cache = MLA(
            model_dimension=self.model_dimension,
            n_heads=self.n_heads,
            T=self.T,
            latent_dim=self.latent_dim,
            dhR=self.dhR,
            model_dtype=self.model_dtype,
            dropout=self.dropout_rate,
        )(x, KV_cache=cache[0], KR_cache=cache[1], train=train)
        x = x + x_res
        x_res = x

        x = RMSNorm(model_dtype=self.model_dtype)(x)
        x = FeedForward(
            model_dimension=self.model_dimension,
            dropout_rate=self.dropout_rate,
            model_dtype=self.model_dtype,
        )(x, train=train)
        x = x + x_res

        return x, cache

We can now just call $n$ layers per block.

class Block(nn.Module):
    layers: int
    model_dimension: int
    n_heads: int
    T: int
    latent_dim: int
    dhR: int
    dropout_rate: float = 0.1
    model_dtype: jnp.dtype = jnp.bfloat16

    @nn.compact
    def __call__(
        self, x, cache: Optional[cache_type] = None, train=True
    ) -> Tuple[Array, cache_type]:
        KV_cache = []
        KR_cache = []

        for i in range(self.layers):
            current_cache = [None, None]
            if cache is not None:
                current_cache[0] = cache[0][i]
                if i < self.layers - 1:
                    current_cache[1] = cache[1][i]

            x, cache_out = Layer(
                model_dimension=self.model_dimension,
                n_heads=self.n_heads,
                T=self.T,
                latent_dim=self.latent_dim,
                dhR=self.dhR if i < self.layers - 1 else 0,
                dropout_rate=self.dropout_rate,
                model_dtype=self.model_dtype,
            )(x, current_cache, train=train)

            ckV, kRT = cache_out
            if ckV is not None:
                KV_cache.append(ckV)
            if kRT is not None:
                KR_cache.append(kRT)

        KV_cache = jnp.stack(KV_cache, axis=0) if len(KV_cache) > 0 else None
        KR_cache = jnp.stack(KR_cache, axis=0) if len(KR_cache) > 0 else None

        out_cache = (KV_cache, KR_cache)

        return x, out_cache

We keep an array for the two separate caches appending if the cache is not None and further stacking to make them into JAX Arrays.

Transformer Model

Forward Pass and Caching

We can now write the final Transformer Model essentially looping through $n$ blocks.

The first step is to check if the cache input is not None, as that indicates we only want the last token. We can then reshape the input into a (B, T) tensor.

class Transformer(nn.Module):
    model_dimension: int
    vocab_size: int
    n_head: int
    blocks: int
    layers_per_block: int
    T: int
    latent_dim: int
    dhR: int
    dropout_rate: float = 0.1
    model_dtype: jnp.dtype = jnp.bfloat16

    @nn.compact
    def __call__(
        self, x, cache: Optional[cache_type] = None, train=True
    ) -> Tuple[Array, cache_type]:
        if cache is not None:
      x = x[..., -1:]

        *B, T = x.shape
        x = x.reshape(-1, T)

We then add our embedding module and go through the self.blocks. In the end, we apply the embedding again but use the out=True to perform the weight tying. Finally, we reshape into the original size. The final transformer block is shown below.

class Transformer(nn.Module):
  embedding = Embedding(
    vocab_size=self.vocab_size,
    model_dimension=self.model_dimension,
    model_dtype=self.model_dtype,
  )

  x = embedding(x)

  KV_cache = []
  ckRT_cache = []

  for i in range(self.blocks):
    if cache is None:
      layer_cache = None
    else:
      cKV = cache[0][i]
      kRT = cache[1][i] if cache[1] is not None else None
      layer_cache = (cKV, kRT)

    x, cache_out = Block(
      layers=self.layers_per_block,
      model_dimension=self.model_dimension,
      n_heads=self.n_head,
      T=self.T,
      latent_dim=self.latent_dim,
      dhR=self.dhR,
      dropout_rate=self.dropout_rate,
      model_dtype=self.model_dtype,
    )(x, layer_cache, train=train)

    if cache_out[0] is not None:
      KV_cache.append(cache_out[0])
    if cache_out[1] is not None:
      ckRT_cache.append(cache_out[1])

  if len(KV_cache) > 0:
    KV_cache = jnp.stack(KV_cache, axis=0)
  else:
    KV_cache = None
  if len(ckRT_cache) > 0:
    ckRT_cache = jnp.stack(ckRT_cache, axis=0)
  else:
    ckRT_cache = None
  out_cache = (KV_cache, ckRT_cache)

  x_out = embedding(x, out=True)
  x_out = x_out.reshape(*B, T, self.vocab_size)

  return x_out, out_cache

Configuration and Initialization

This is not the final model we are using for training since in native JAX, it is not simple to split across n-D parallelism and we want to stay away from abstractions provided by Flax which operate as a blackbox over the network. To simplify construction of the transformer, we can create a data class to represent the arguments to the constructor and create a static method that will load the transformer.

dtype_map = {
    "bfloat16": jnp.bfloat16,
    "float32": jnp.float32,
    "float16": jnp.float16,
    "int32": jnp.int32,
    "int64": jnp.int64,
}

def convert_dtype(dtype_str):
    if dtype_str in dtype_map:
        return dtype_map[dtype_str]
    else:
        raise ValueError(f"Unsupported dtype: {dtype_str}")

@dataclass
class modelConfig:
    """model config class"""

    model_dimension: int
    vocab_size: int
    n_head: int
    blocks: int
    layers_per_block: int
    T: int
    latent_dim: int
    dhR: int
    dropout_rate: float = 0.1
    model_dtype: str = "bfloat16"

class Transformer(nn.Module):
  ...
  @classmethod
    def get_model(cls, cfg: modelConfig) -> "Transformer":
        return cls(
            model_dimension=cfg.model_dimension,
            vocab_size=cfg.vocab_size,
            n_head=cfg.n_head,
            blocks=cfg.blocks,
            layers_per_block=cfg.layers_per_block,
            T=cfg.T,
            latent_dim=cfg.latent_dim,
            dhR=cfg.dhR,
            dropout_rate=cfg.dropout_rate,
            model_dtype=convert_dtype(cfg.model_dtype),
        )

We next discuss how to apply parallelism methods to scale this transformer.